
Binary Number System
Begineers Simple Introduction To Binary Number System
The binary number system is a fundamental concept in computer science and digital electronics. Unlike the decimal system that we commonly use in our everyday lives, which is based on powers of 10, the binary system operates on powers of 2.
Whereas, the binary system, only two digits, 0 and 1, are used to represent numerical values. This system serves as the foundation for all digital computing and is integral to the language of computers.
Understanding the binary number system is foundational for anyone involved in computer science, digital electronics, or programming. It forms the basis for how information is stored, processed, and communicated in the digital world.
The Computer system understands only Binary Number System . Therefore, we need to communicate with the computer only using Binary Code also referred to as machine instructions.
The binary code is also alternately referred as machine language or machine code. In binary number system, all the number are represented by using only two numeric numbers that is either 0 ( zero ) or 1 ( one ).
All computer programs written in any high level programming language must be first converted into machine code in binary that can be directly executed by the computer’s central processing unit – CPU.
In this lesson, we will discuss in detail and find the answers to some important topics in binary number system.
These questions include , why computer understands only Binary code, why binary code consist of only two numbers that is 0 ( zero ) and 1 ( one ) , different types of number systems , what are logic gates and Boolean algebra.
How Computer Works ?
Binary Numbers System
Table Of Contents
Binary Numbers System And Logic Gates
Interview Questions
- What Is Binary Number System ?
- What are different types Number Systems ?
- Why Computer System Use Only Binary Number System ?
- Why Computer Programs are Compiled ?
- How Data Is Represented In Binary ?
- Binary Code And Binary Units
- Binary Number And Logic Gates
- Binary Number And Boolean Algebra
Learning Computer science is now considered to be one of the best career option . The career in Computer Science not only offers an opportunity to work with some top notch corporate companies but also to work as an entrepreneur.
The Computer Science career also offers you an opportunity to put your career on the fast track with excellent financial rewards .
What Is Number System ?
We are all familiar with the commonly used numerical number system ( Decimal Number System that makes use of digits from 0 to 9 ) that we all use in our daily life.
However, there are many number system exist that can be used while communicating with the computer system and supported by most computer programming languages .
A numbering system is a system followed to define a set of values used to measure a quantity . With the help of numbering system , we can express the quantitative dimension of any object.
For example , to express weight 75 kg , Age as 26 Years , Distance as 100 KM and so on.
However, due to its system hardware architecture of the computer system, the commonly used decimal numerical number system is not suitable.
Due to computer hardware architecture constrains, the decimal system cannot be implemented for the functioning of the computer system.
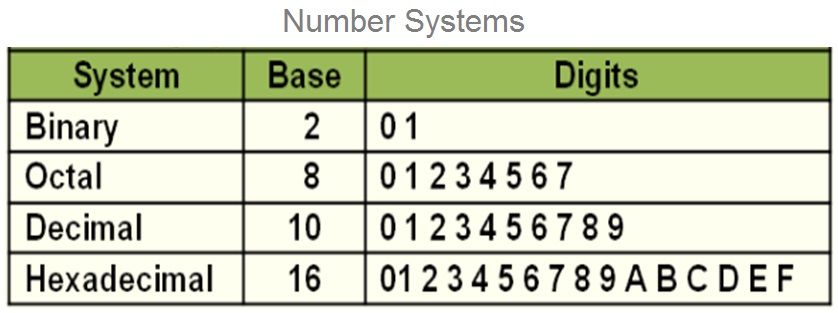
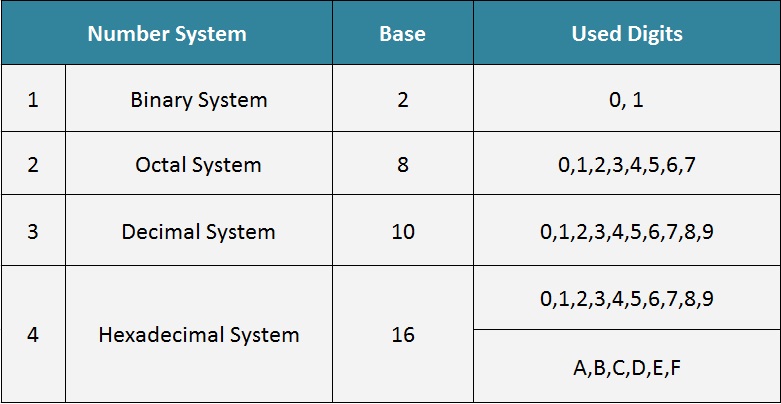
Types Of Number System
A number system is defined as a system that allows to represent any number using a set of combination of symbols, digits and alphabets. The CPU of the computer system can interpret and execute only machine code instructions in Binary .
And therefore , all program code in any language must be converted to machine code in binary with the help of compiler . However , most programming languages support these four number system while writing a program code.
Binary Number System
A Binary number system makes use of only two digits that is 0 and 1. In Binary Number system any number is represented by using only two digits that is 0 and 1 .
The binary number system has base of 2, because it has only two digits to represent any number.
Octal Number System
The Octal number system makes use of only eight ( 8 ) digits from 0 to 7 to represent any number. In Octal number system any number ( value ) can be represented with combination of any 8 digits ( 0,1,2,3,4,5,6, 7 ).
The octal number system has a base of 8, because it has only 8 digits to represent any number
Decimal Number System
The Decimal number system is the most commonly used number system which makes use of ten ( 10 ) digits from 0 to 9 to represent any number.
In decimal system any number can be represented with the combination of 10 digits ( 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 ). The decimal number system has a base of 10, because it has 10 digits to represent any number
Hexadecimal Number System
The Hexadecimal number system has sixteen ( 16 ) alphanumeric values from 0 to 9 and A to F to represent any number.
The Hexadecimal number system makes use of nine ( 10 ) digits ( 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 )and seven ( 6 ) alphabets ( A, B, C, D, E, F ) to represent any number in this number system.
The hexadecimal number system has a base of 16, because it makes use of 16 alphanumeric values.

Binary Number System
In mathematics and digital electronics , a binary number is a number expressed using binary numeral notation system or base – 2 numeral system .
The binary number system represents any numeric values by using combination of only two possible values that is 0 ( zero ) and 1 ( one ) . In digital electronics this is best suited to represent two states ON or OFF .
The Binary number system uses only two digits to represent any number . Because of its straightforward implementation in digital electronic circuitry using logic gates, the binary system is used internally by almost all modern computers and computer-based devices.

And therefore , computer system is a digital electronic device which can understand and execute program instructions communicated in terms of two states ON or OFF . These two states can be best represented using binary number system.
Why Computer Use Binary Number System ?
The computers were invented due to their high computing ability . The computers are used to process large volumes of data at lightning speed . The computer system consist of number of components .
Each of these component perform a specific task . One of the most important component in a computer system is CPU.
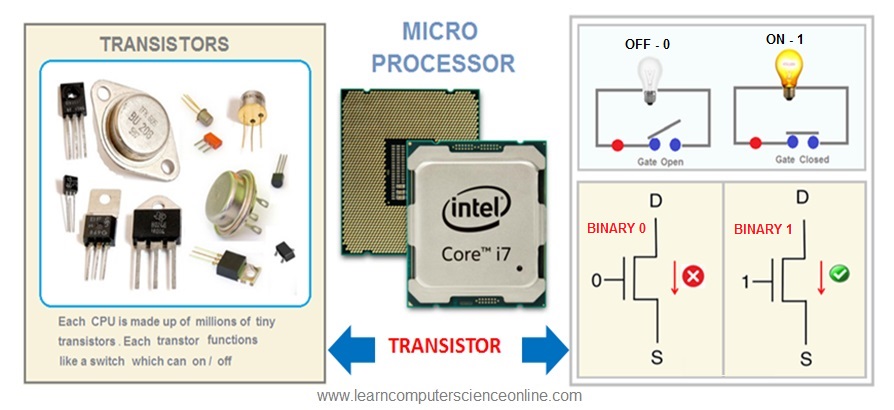
The CPU ( Central Processing Unit ) within a computer system is responsible to perform all the arithmetic calculations and logical decisions.
The CPU is also referred as microprocessor Or processor chip Or simply as processor.
The processor chip consist of millions of tiny electronic component called Transistor . The transistor is a fundamental building block for all digital electronic gadgets including computers.
The transistor is made-up of silicon which is a semiconductor material . The transistors are used as a micro switch that can be either switched ON or switched OFF .
The computer’s processor , which is the brain of the computer system consist of millions of these transistors .
And hence , the computer processor can understand and execute instructions communicated in the form of only two states that is switch on Or off.
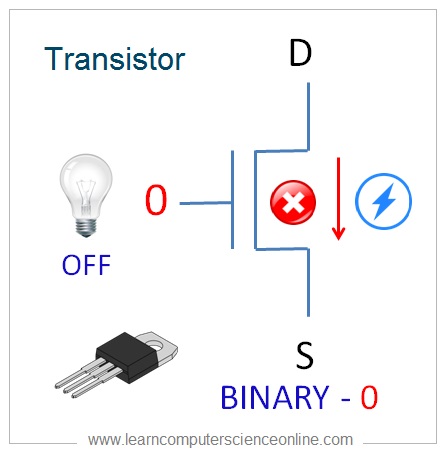
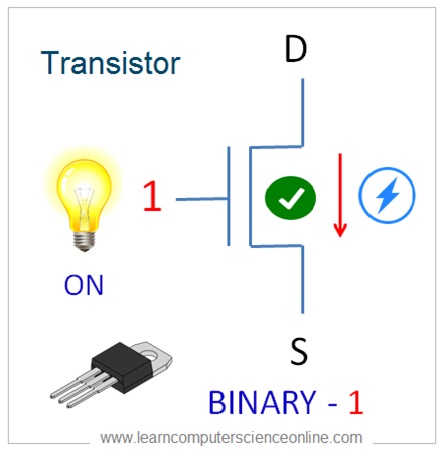
And therefore , to communicate with computer system , we need a number system that is capable of representing any number using only two digits .
The binary number system perfectly fits in to this condition because in binary number system we make use of only two digits that is 0 and 1.
In Binary , the switched ON state is represented 1 ( one ) and the switched OFF state is represented by 0 ( zero ) .
And for this reason computer architecture supports binary number system and all computer programs must be first compiled into machine code instructions in binary which computer CPU can execute.
Why Computer Use Binary Number System ?
How Data Is Represented In Binary ?
The Computer stores all information and program data only in binary digital form. That means all the data be it text, photographs, audio , video or whatever else is comprised of only collections of ones and zeroes.
However , the operating system presents this data in a graphical format in GUI environment which is human readable.

Binary Code And Binary Units
Since the computer CPU can execute only machine code instructions and operate on the data in binary , All the program code and the data must be represented in the binary form .
The CPU operates on the data and the result of this operation can be sent to either output device ( monitor , printer etc ) or it can be stored in a permanent storage device for future use.
The fundamental building block of digital information is the binary digit or bit, which represents a single 0 ( zero ) or 1 ( one ) state. This is represented by a bit in computer memory which is the smallest memory unit.
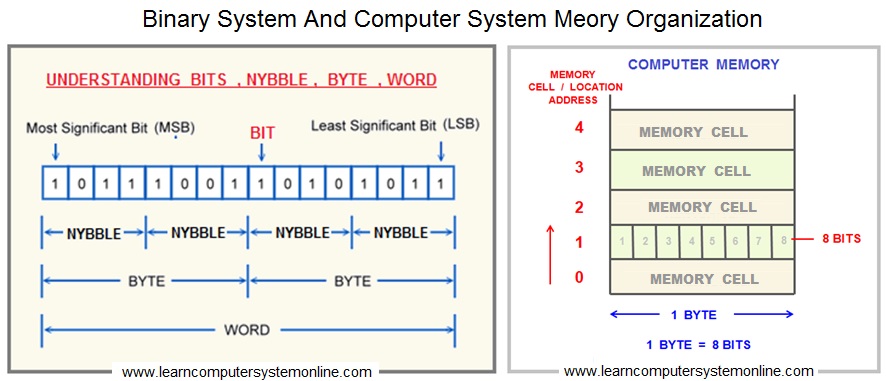
To represent a large amount of data , the bits can be organized into groups of four , eight , sixteen , 32 or 64 bits , called nybbles / nibble , bytes , words, long words and very long words respectively. These are referred as binary units of measurement .
The computers recognize only two discrete states : on and off. These states can be represented by two digits , 0 and 1 . Each 0 or 1 is called a bit in the binary system. A Bit is the smallest unit of data a computer can process.
A Bit is a short for binary digit. The binary system has a base of 2 with the two digits ( 0 and 1 ). By using combinations of 0s and 1s we can represent larger numbers.
Binary Numbers And Logic Gates
The computer system performs different jobs by executing the program instructions as per the program logic . The CPU is the main component inside a computer system which performs all arithmetic calculations and also logical operations .
The Computer CPU is responsible to perform both arithmetic calculation and logical operations. The CPU is made-up of millions of tiny circuits called transistors which can function as micro switch .
The logic gates are constructed by using transistors inside a processor chip mainly used by the CPU to perform logical operations .

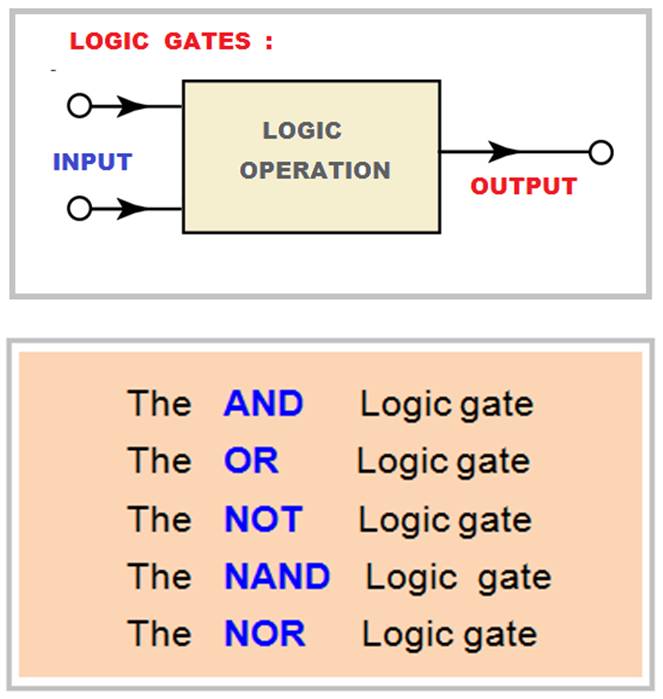
The computers are digital machines and logic gates are the basic components in digital electronics. The Logic gates are used to create digital circuits and even complex integrated circuits.
The computer’s CPU consist of millions these tiny circuits which enable the CPU to perform the logical operations.
The processor works by reacting to an input of 0s and 1s in specific manner and then returning an output based on the decision.
The decision itself happens in a circuit called a logic gate, each of which requires at least one transistor, with the inputs and outputs arranged differently for different operations.
Binary Number And Boolean Algebra
In mathematics and mathematical logic , Boolean algebra is the branch of algebra in which the values of the variables are the truth values ( true and false ) and this is usually denoted in binary 1 and 0 respectively.
The Boolean algebra was introduced by George Boole in 1854 who was a British Mathematician .Boolean algebra has been fundamental in the development of digital electronics .
In algebra we make use of decimal numbers , whereas the Boolean algebra uses truth values , true ( 1 ) and false ( 0 ).
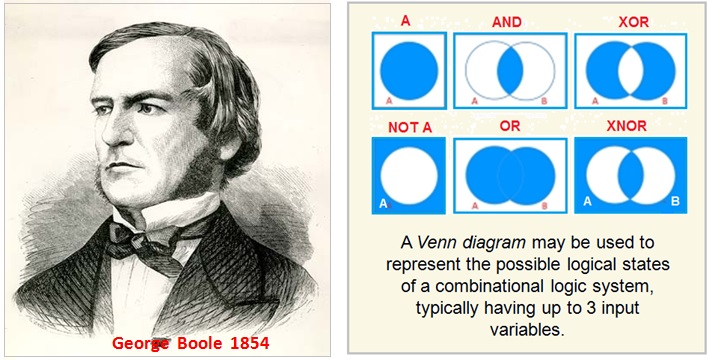
A logic gate is a tiny circuit used in processors for making a logical decision which is based on Boolean algebra .
Boolean Algebra is used to analyze and simplify the digital ( logic ) circuits. It uses only the binary numbers i.e. 0 and 1. It is also called as Binary Algebra or Logical Algebra.
Key Concepts In Binary System
- Binary Digits (Bits):
The binary system uses individual digits called bits (binary digits). Each bit can have one of two values, 0 or 1. Multiple bits are combined to represent more complex information.
- Binary Representation:
In binary, each digit’s position represents a power of 2. The rightmost bit represents 2^0 (1), the next bit to the left represents 2^1 (2), the next 2^2 (4), and so on. This positional notation allows for the representation of any positive integer using only the digits 0 and 1.
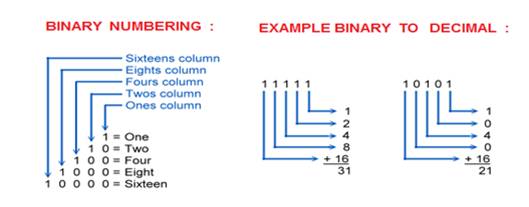
- Conversion from Decimal to Binary:
To convert a decimal number to binary, the process involves repeatedly dividing the decimal number by 2 and noting the remainders. The binary representation is then derived from the sequence of remainders, with the remainder for the least significant bit (rightmost) written first.
Example: To convert 13 to binary:
13÷2=6 (remainder 1)6÷2=3 (remainder 0)3÷2=1 (remainder 1)1÷2=0 (remainder 1)13÷26÷23÷21÷2=6 (remainder 1)=3 (remainder 0)=1 (remainder 1)=0 (remainder 1)
So, the binary representation is 1101.
- Binary Arithmetic:
Binary arithmetic involves addition, subtraction, multiplication, and division using binary numbers. Addition in binary follows similar principles to decimal addition, but with a carry-over occurring when the sum in a position is 2.
Example: Adding 1101 and 101:
1101+11011100+111110110100
- Binary to Decimal Conversion:
Converting a binary number to decimal involves multiplying each bit by the corresponding power of 2 and summing the results.
Example: Converting 1101 to decimal:
1×23+1×22+0×21+1×20=8+4+0+1=131×23+1×22+0×21+1×20=8+4+0+1=13
Applications Of Binary Number System
- Digital Computing:
Computers use the binary system internally for all data storage and processing. Instructions, data representation, and memory storage in computers are based on binary.
- Digital Communication:
Binary encoding is prevalent in digital communication systems, such as telecommunications and networking. Information is transmitted and stored digitally using binary code.
- Logic Gates and Circuits:
Digital circuits, including logic gates and microprocessors, rely on binary representation for performing computations and making decisions.
- Machine Language:
In computer programming, machine language instructions are represented in binary. Assembly language and higher-level programming languages are eventually translated into binary machine code for execution.
Join The Best Seller
Computer Science Online Course
This is the most comprehensive and unique Computer Science And Programming Fundamentals course Online which will give you in depth understanding of most important fundamental concepts in computer science And Programming .


