Database Keys
Introduction to Database Keys
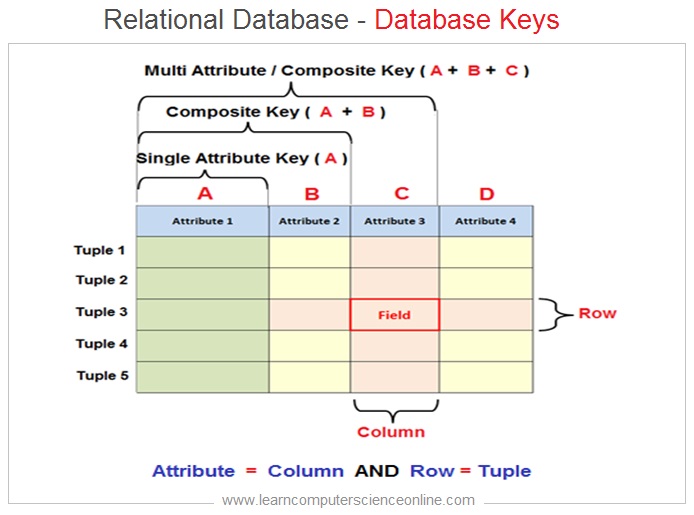
The database key is an attribute or a group of attribute that can uniquely identify each record in a table . The keys are an important feature of a relational table.
In relational database model , the logical structure of the database is represented by the number of interrelated tables.
The DBMS access the data field in the table with reference to the table row and column. And therefore , each record ( row ) in a table is uniquely identified with the help of a key.
The relational model makes user of different types of database keys to define and establish the relationship between the various tables.
In this tutorial , you will learn what is a key in DBMS , different types of keys and how these keys are defined and used during the database design stage.
This tutorial will help you understand some important related topics such as table structure , primary key , foreign key , candidate key , composite key and other related topics.
What Are Database Keys ?
Database Keys And Relational Model
The term database key is used in the context of relational databases. The relational database is based on the relational model proposed by British computer scientist E F Codd.
In order to understand the concept of database keys , it is important to have a reasonably good understanding of the relational database model .
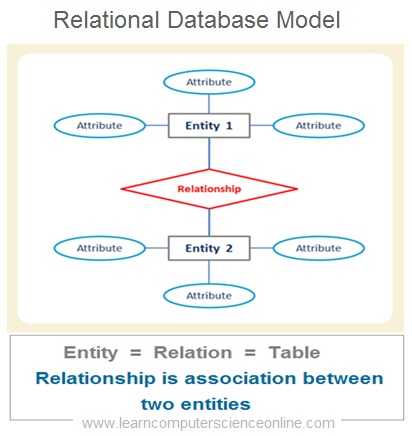
In relational database model , the logical structure is a database is represented as group of interrelated tables. Each table represents a database entity .
Relational Model
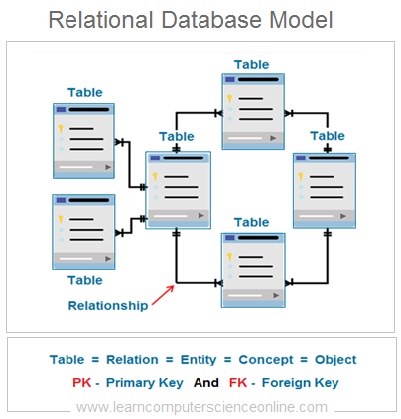
Relational Table
The database entity is an object or a business concept that needs to be represented into the database so that we can store the related data.
For example, the college database will have student, teacher, courses, and the department are some of the valid entities.
Each database entity will have some attributes. An attribute highlight a specific feature of the entity.
For example, the student entity can have first name , last name , student ID , email address , date of birth are valid attributes.
Entity Relationship Diagram
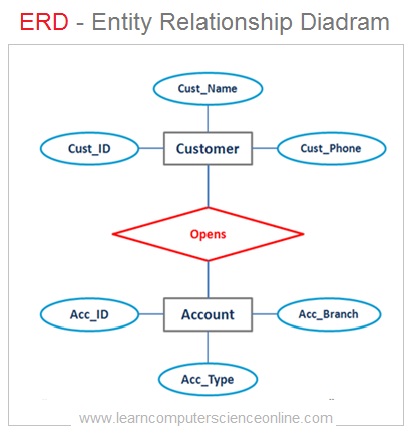
Relational Database Model
What Are Database Keys ?
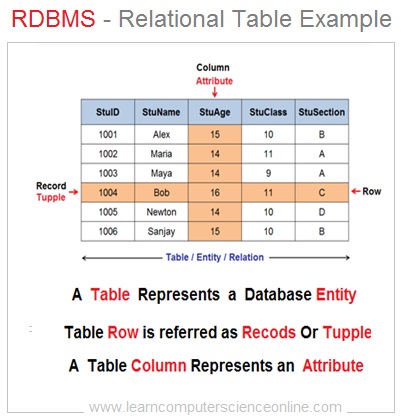
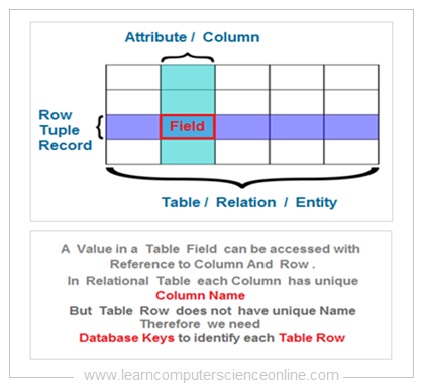
A database key is defined as either a single attribute or group of attributes can uniquely identify each record ( row or tuple ) in a table.
Each table represents a single database entity. A table in relational model has rows and columns . The table columns represents the attributes of the entity.
Whereas, the table row ( also referred as record or tuple ) represents an instance of the entity. For example, In the student table each tuple contains a record pertaining to one specific student.
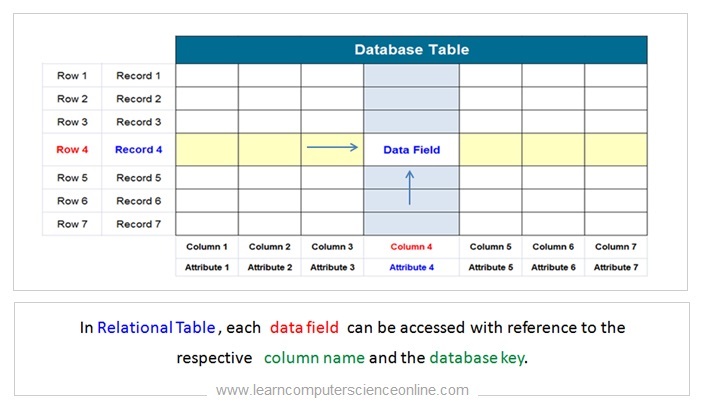
The data is stored ( logically ) into the data field which is an intersection of table row and column . Each data element in a table can be accessed with reference to the specific row and column.
In the table, each column have unique name ( attribute name ) but the table row does not have a unique name . And therefore , we need to define a database key so that each row in a table can be uniquely identified.
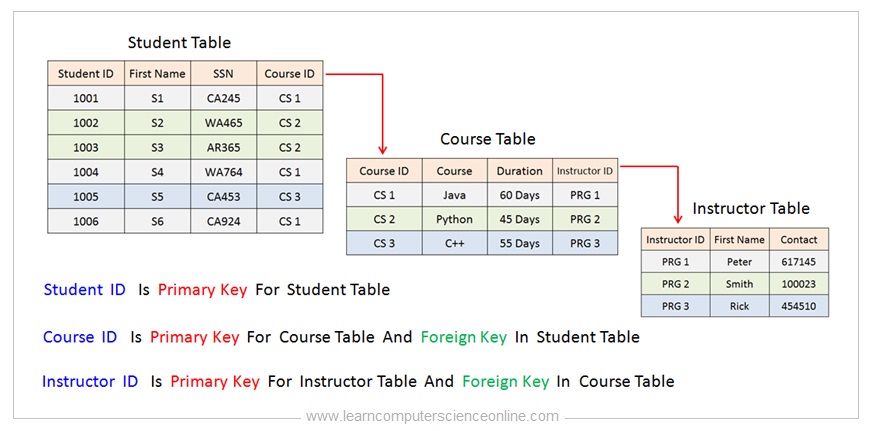
A table key can be a unique single attribute such as student ID , employee ID , SSN ( Social Security Number ) that has a unique value for each row in a table.
If the table does not contain a unique attribute that can used as database key then the combination of two or more attribute can be used to define the database key for that table. Such key is referred as composite key.
What Is The Use Of Database Keys ?
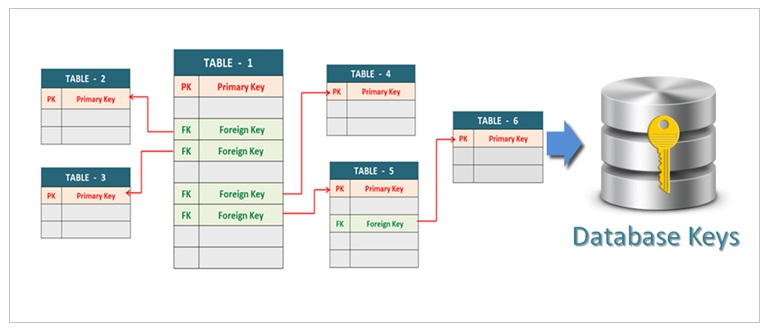
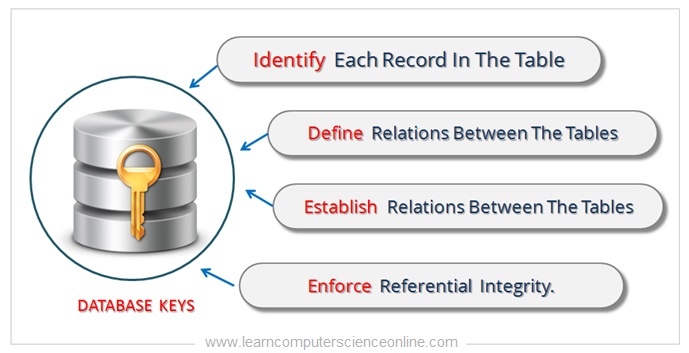
The main use of the database key is to individually identify each record in a table . The database key are used to establish and define the relationship between the tables.
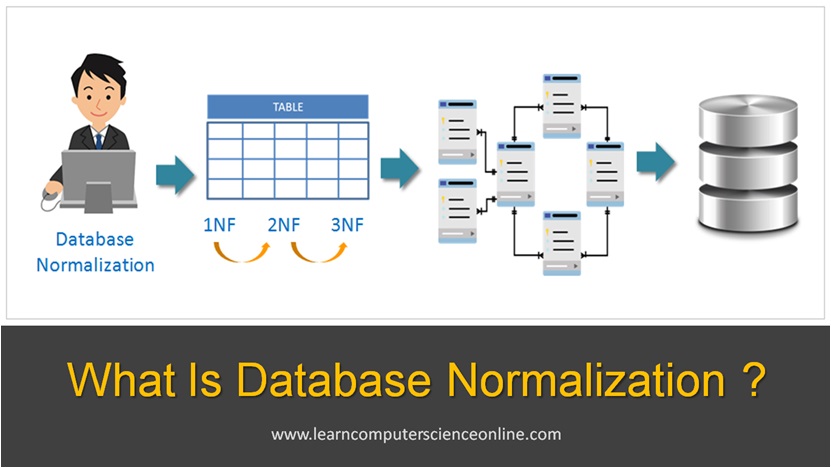
During the database design stage, the database designers decompose the larger database tables into smaller tables that contains data related to single entity. This technique is referred as database normalization.
The larger tables with data of multiple entities create the problems due to data redundancy such as database anomalies. And therefore, database normalization is an important step in the database design.
The database keys plays an important role by establishing the relationship between the two tables. The relationship between the tables ensures that the referential integrity is enforced.
Types Of Database Keys
The database key types can be broadly grouped into two groups. The first group of keys include unique keys and the second group is non-unique keys.
A database key is said be unique when it has a unique value for each row ( that is tuple / record / instance ).
A database key is said be non-unique when a unique key of one table is used in another table with non-unique value for the purpose of defining a relationship between the two tables.
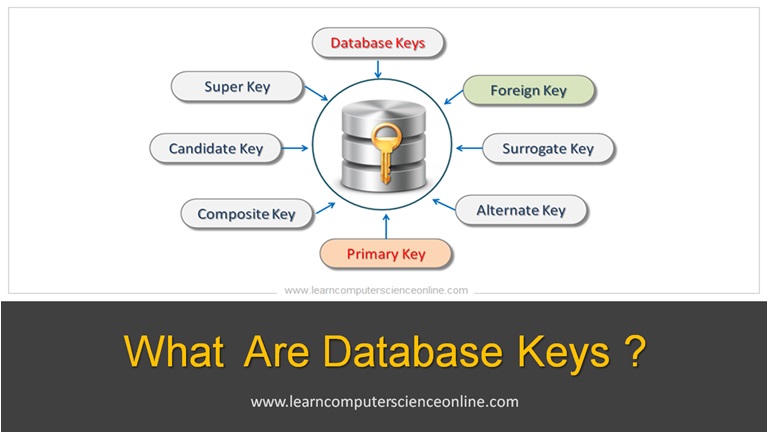
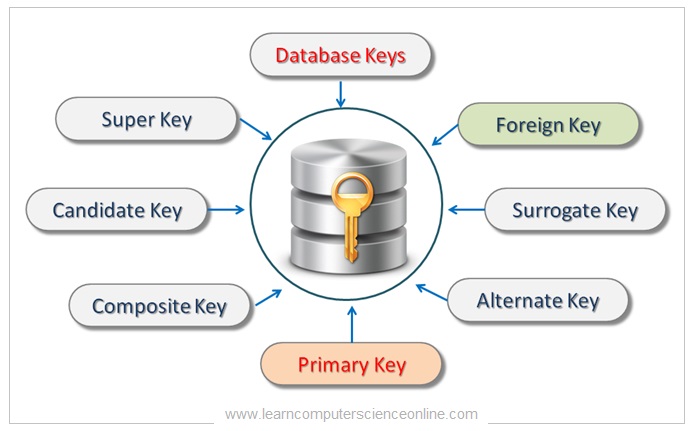
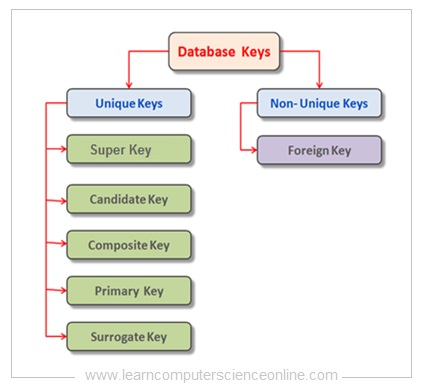
The different types of database keys used in relational model include :
Database Key Types
- Super Key.
- Candidate Key.
- Primary Key.
- Foreign Key.
- Composite Key.
- Surrogate Key.
What Is Super Key ?
Definition Of Super Key
The term super key is defined as either a single attribute or group of attribute that can be used to uniquely identify each row in a table.
The super key is the most general form of unique key. The table can have many super keys. A set of super keys is usually a superset for other keys.
In the context of database design, the database designers will first identify number of super keys in a relation for a given functional dependencies.
The next step is to identify the set of candidate keys and then select the primary key from the set of candidate keys.
In other words , a primary key is always a candidate key and also a super key but the reverse is not true.
Super Key Example
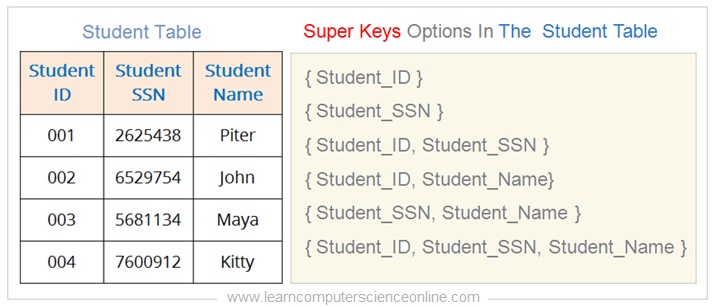
Let us understand the the concept of super key with one simple example. In this example, we will identify super key for the following student table.
Student_ID | Student_SSN | Student_Name |
001 | 2625438 | Peter |
002 | 6529754 | John |
003 | 5681134 | Maya |
004 | 7600912 | Kitty |
In this example, the Student Table has following six number of super keys that can uniquely identify each record in the student table.
- { Student_ID }
- { Student_SSN }
- { Student_ID, Student_SSN }
- { Student_ID, Student_Name}
- { Student_SSN, Student_Name }
- { Student_ID, Student_SSN, Student_Name }
The attributes Student_ID and Student_SSN will always have unique values for each instance of the student table . And therefore, both these attributes qualify for the super key.
Whereas , the Student_ Name attribute cannot be considered for a super key because its unique value cannot be guaranteed. For example , the student table can have many students with Peter name.
However , the Student_ Name attribute can be used in a composite key in combination with either Student_ID and Student_SSN or both together.
What Is Candidate Key ?
Definition Of Candidate Key
The term candidate key is defined as super key with minimum number of attributes. In other words , a candidate key is super key without any redundant attribute.
The main purpose of the candidate key is to offer multiple options to the database designers so that suitable primary key can be selected.
The candidate keys are selected from a set of super keys with minimum number of attributes and usually a sub set of super key.
In the context of database design , the database designers will identify the candidate keys from the set of super keys in a relation for a given functional dependencies.
Each candidate key can effectively function as primary key but the database designers must select one of the candidate key as primary key.
In other words , a primary key is always a candidate key and also a super key but each candidate key need not be a primary key. Because we need to select only one candidate key as a primary key.
Similarly , each candidate key is a super key but each super key need not be a candidate key.
Candidate Key Example
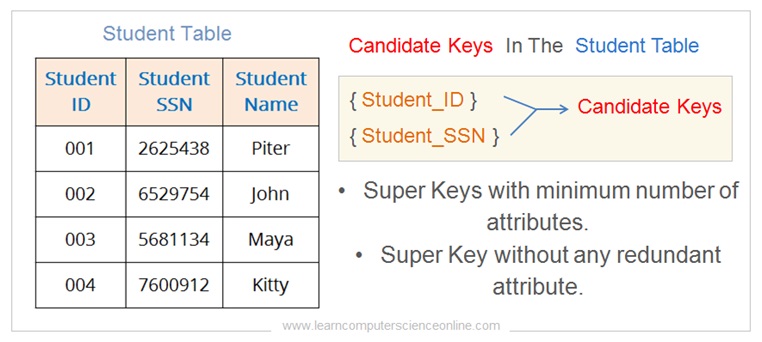
Let us understand the concept of candidate key with one simple example.
We will use the same table that we have used in the previous example. Let us now identify the candidate key from the set of super keys for the following student table.
Student_ID | Student_SSN | Student_Name |
001 | 2625438 | Peter |
002 | 6529754 | John |
003 | 5681134 | Maya |
004 | 7600912 | Kitty |
The Student table has following number of super keys that can uniquely identify each record in the student table.
Amongst the set of six super keys , now we need to identify candidate key options that has minimum attributes.
And therefore , following two super key satisfy the criterion to qualify as candidate key.
- { Student_ID }
- { Student_SSN }
Following super key options does not qualify to be a candidate key because both Student_ID and Student_SSN individually qualify to be a proper subset of this composite key.
- { Student_ID, Student_SSN }
Similarly , remaining super key options also does not satisfy the minimum attribute criterion and hence cannot be considered for the candidate key.
What Is Primary Key ?
Definition Of Primary Key
The term primary key is defined as a database key that is selected by the database designer ( or database administrator ) as a primary key for a given relational table.
A table can have only one primary key. And therefore, the database designer can select any one of the candidate key as a primary key.
The main purpose of the primary key is to uniquely identify reach row ( record ) in a relational table.

The primary key with its unique value for each row is used to access each data field in a table with reference to the respective primary key attribute and column name.
Both the candidate keys qualify to be a primary key . And therefore , the database designer can select the primary key from any one of the following two candidate keys.
- { Student_ID }
- { Student_SSN }
What Is Foreign Key ?
Definition Of Foreign Key
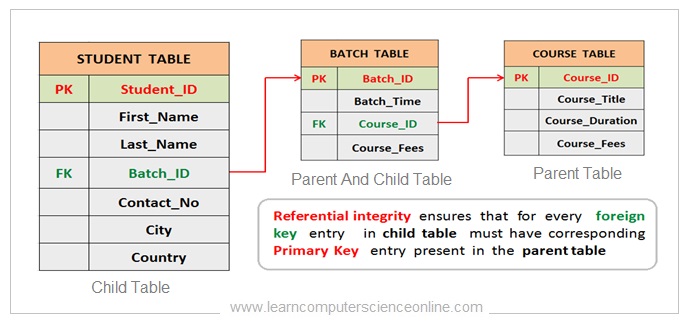
When the primary key of one table ( Also referred as Parent Table ) is included as a non-unique attribute into another table ( Also referred as Child table ) then such database key is referred as foreign key.
The main purpose of the foreign key is to create and define the relationship between the two tables.

The foreign key constrain is an important feature of the relational database design to enforce the referential integrity.
The referential integrity ensures that for every foreign key field in a child table there must be a corresponding table with same attribute as a primary key.
The referential integrity plays an important role in the relational database to ensure the accuracy and the consistency of the data.
The main purpose of the foreign key is to create and define the relationship between the two tables.
What Is Composite Key ?
Definition Of Composite Key
The composite key is defined as a database key that is consist of more than one prime attribute.
The database designer use composite key option when a single attribute primary key option is not available. In such situation the composite key is as a primary key.
What Is Surrogate Key ?
Definition Of Surrogate Key
In order to understand the concept of surrogate key , we need to first understand the concept of Natural Key.
A natural key is defined using the existing attributes present in the database table and redundant attribute is not added to the table for the purpose of defining a primary key.
In other words, the attributes that are part of the natural key have contextual meaning that can be related to any business entity for which the database is being developed .
And therefore, a part of the natural key will be selected by manual action even if the natural key is system generated .
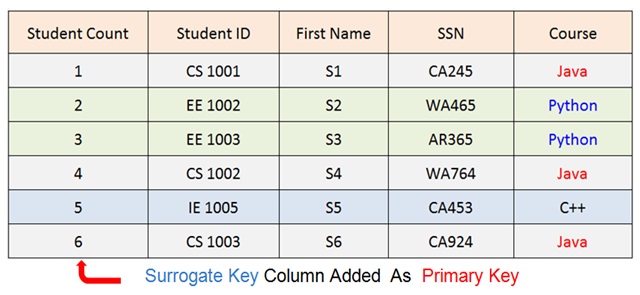
On the contrary , A surrogate key is not a natural key because surrogate key attribute is specifically added to the table as a prime attribute for the purpose of defining the primary key.
The most common and frequently used example of the surrogate key is the auto generated integer values in the increasing sequential order ( such as 1, 2, 3 , 4 , 5 ).
Join The Best Seller
Database Design Online Course
Learn database design and development step by step. This is the most comprehensive and unique Database Design course Online.
This course will give you in depth understanding of most important fundamental concepts in database design with MySQL project.